Home
Research
Teaching
Publications
Group
Press
Presentations
QED
Contact
Search
Menu Menu

Link to X
Link to Google_scholar

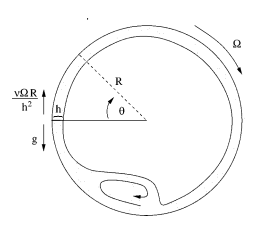
Axial instability of a free-surface front in a partially-filled horizontal rotating cylinder,

Axial instability of a free-surface front in a partially-filled horizontal rotating cylinder

https://softmath.seas.harvard.edu/wp-content/uploads/2019/10/252.png 229 267 Academic Web Pages /wp-content/uploads/2018/09/clear.png Academic Web Pages1999-10-06 13:52:002025-02-27 15:13:14Axial instability of a free-surface front in a partially-filled horizontal rotating cylinder

Recent Publications

Stigmergic optimal transport

Hamiltonian bridge for scale-dependent optimal control of particles and fields

Optimal bioelectric control accelerates collective wound healing

Surface wakes on ultra-soft solids

Courtship vocalizations in male ducks: spectral composition and resonance of the syringeal bulla

Distributed neural computation and the evolution of the first brains

Self-organized adaptive branching in frangible matter

Reversible superdeformability of hiPSC epithelial cortinoids

General integrated rate law for complex self-assembly reactions reveals the mechanism of amyloid-beta coaggregation

Viscous adhesion in vibrated sheets: elastohydrodynamics with inertia and compressibility effects

Harvard John A. Paulson School of Engineering and Applied Sciences
Harvard Department of Physics
Harvard Department of Organismic and Evolutionary Biology

Prof. L. Mahadevan
Pierce Hall 322
Harvard University
29 Oxford Street
Cambridge, MA 02138
lmahadev@g.harvard.edu
(617) 496-9599

Follow us on Twitter

© Copyright L. Mahadevan. Site by Academic Web Pages

Link to X
Link to Google_scholar

Login
For Lab Members

Fluid rope trick investigated

Fluid rope trick investigated

Propagating fronts on sandpile surfaces,

Propagating fronts on sandpile surfaces,